The Ant Problem

Image by mi_shots Today we’ll be looking at a classic problem in probability: “The Ant Problem”.

The Question:

An ant leaves its anthill in order to forage for food. It moves with the speed of 10cm per second, but it doesn’t know where to go, therefore every second it moves randomly 10cm directly north, south, east or west with equal probability.

a) If the food is located on east-west lines 20cm to the north and 20cm to the south, as well as on north-south lines 20cm to the east and 20cm to the west from the anthill, how long will it take the ant to reach it on average?

b) What is the average time the ant will reach food if it is located only on a diagonal line passing through (10cm, 0cm) and (0cm, 10cm) points?

c) Can you write a program that comes up with an estimate of average time to find food for any closed boundary around the anthill? What would be the answer if food is located outside an defined by ( (x – 2.5cm) / 30cm )2 + ( (y – 2.5cm) / 40cm )2 < 1 in coordinate system where the anthill is located at (x = 0cm, y = 0cm)? Provide us with a solution rounded to the nearest integer.

The question can be found here.

Solutions:

Part A:

Let’s demonstrate the solution of this problem with probability.

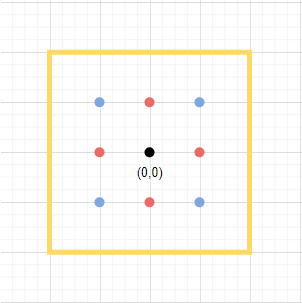
Figure 1.

Given that the ant starts at the origin, we can see from Figure 1 that the ant has four options: up, right, down, and left (corresponding to the red dots in Figure 1). Notice that taking any of these four routes places the ant in one of four equivalent positions. These positions are considered equivalent because, from any of them, the ant has the same possibilities for the next step. Similarly, if the ant lands on any blue points, there are three other equivalent positions within the grid where the possible next steps are exactly the same.

Let $X_{\text{black}}, X_{\text{red}},$ and $X_{\text{blue}}$ denote the random variables representing the number of steps required to reach the yellow box from the black, red, and blue points, respectively. These can also be expressed as:

Taking the expectation of the 3 random variables gives:

Solving the above formulas by substitution gives:

Therefore, on average it will take the ant 4.5 steps to reach the food.

This solution can be verified using the code from the last section.

Part B:

The premise behind this question is to model the ants 2D random walk as a 1D random walk.

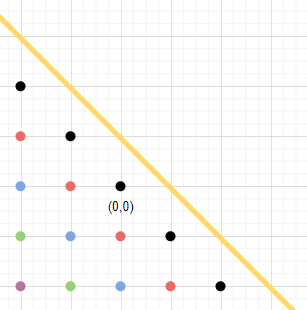
Figure 2.

Let the yellow line denote where the food is located and let $X_{\text{black}}, X_{\text{red}}, X_{\text{blue}}, X_{\text{green}},$ and $X_{\text{purple}}$ denote the random variables modelling the ants walks starting from the black, red, blue, green, and purple points.

Notice at each colour, the ant either moves 1 step further from the line w.p. 1/2 or 1 step closer to the line w.p. 1/2. Consequently, this 2 dimensional walk could be represented as 1D walk.

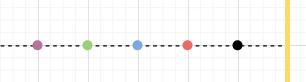
Figure 3.

There are several ways to prove the expected number of steps, and we’ll use a proof by contradiction.

Suppose that the average number of steps to move from the black point to the line exists and is equal to $x$. Next, we’ll construct an equation for $x$ based on the expected number of steps required to return from our starting point. Taking a step toward the yellow lines gives us 1 step, and from there, no further steps are needed. On the other hand, taking a step toward the red point initially adds 1 step. From the red point, we then need to find the expected number of steps to return to the black point and subsequently reach the yellow line. The expected number of steps from the red point to the black point is equivalent to the number of steps from the black point to the yellow line. From our initial assumption, we know that the expected number of steps for this is $x$. Similarly, starting from the black point, it takes, on average, another $x$ steps to reach the yellow line.

This leads to a contradiction. Consequently, there cannot be a finite average number of steps to hit the yellow line.

The original proof by contradiction can be found here and this solution will be verified in the last section.

Part C:

For this section we will be using python. We’ll create a base class and 3 separate subclasses to verify solutions for the last 3 questions. Each subclass has a custom function called “check” which checks if there is food located at the ant’s current location.

class base_ants:
	def __init__(self, n_iters=100000, max_iters=2000):
		self.n_iters = n_iters
		self.max_iters = max_iters

	def estimate(self):
		walk_storage = [self.walk((0,0), 0) for _ in range(self.n_iters)]
		return round(sum(walk_storage) / self.n_iters, 1)

	def check(self, pos):
		pass

	def walk(self, pos, count):
		if count >= self.max_iters:
			return float('inf')

		x, y = pos
		dx, dy = random.choice([(0,10), (10,0), (0,-10), (-10,0)])
		nx, ny = x + dx, y + dy

		if self.check((nx, ny)):
			return count + 1
		else:
			return self.walk((nx, ny), count + 1)

class ants_q1(base_ants):
	def __init__(self):
		super().__init__()

	def check(self, pos):
		x, y = pos
		return abs(x) >= 20 or abs(y) >= 20

class ants_q2(base_ants):
	def __init__(self):
		super().__init__()

	def check(self, pos):
		x, y = pos
		return (x + y) == 10

class ants_q3(base_ants):
	def __init__(self, ellipse_center, horizontal_radius, vertical_radius):
		super().__init__()
		self.ellipse_center = ellipse_center
		self.horizontal_radius = horizontal_radius
		self.vertical_radius = vertical_radius

	def check(self, pos):
		x, y = pos
		x0, y0 = self.ellipse_center
		ellipse_eq = ((x - x0) / self.horizontal_radius) ** 2 + ((y - y0) / self.vertical_radius) ** 2

		return ellipse_eq >= 1

Running the ants_q3 class gives an answer of 14.0.

References:

Random (2021). Random walk 1D with a single bound. [online] Mathematics Stack Exchange. Available at: https://math.stackexchange.com/questions/4320314/random-walk-1d-with-a-single-bound [Accessed 28 Aug. 2024].

‌