The Drunkard
Suppose someone has had a heavy evening in the pub and upon leaving the pub they have somehow ended up by the side of a cliff. Since he has one a one too many drinks he can’t walk well and they now has 1/3 probability to walk off the edge of the cliff or 2/3 probability to take a step backwards. What is the probability that he will eventually fall off the edge of the cliff?
To determine the solution to this problem, we will denote $p_{1}$ as the probability he falls off the cliff given he is one step away, $p_{2}$ the probability he falls off the cliff given he is 2 steps away, etcetera.
Writing $p_{1}$ in terms of the forward and backward steps gives:
$$p_{1} = \frac{1}{3} + \frac{2}{3}p_{2}.$$Similarly, we could write $p_{2}$ as a function of $p_{1}$ and $p_{3}$ and use substitution. However, there will always remain an unknown term. To solve this question, we have to approach this question from another angle. From position 2 we would like to know the probability that the drunkard returns to $p_{1}$ but this is equivalent to the probability the drunkard is at position 1 and reaches position 0, i.e. the structure of this sub-question is the same, just shifted to the right by 1. Next, the probability of reach the cliff from position 1 is independent of the probability of reaching position 1 from position 2.
$$\begin{equation}p_{1} = \frac{1}{3} + \frac{2}{3}p_{2} = \frac{1}{3} + \frac{2}{3}p^{2}_{1}. \end{equation}$$Solving this quadratic equation gives two solutions:
$$p_{1} = \frac{1 \pm \sqrt{1 -8/9}}{4/3} = \frac{1 \pm 1/3}{4/3},$$$$p_{1} = \{\frac{1}{2}, 1\}$$Now we need to determine which of the two probabilities are correct. To do this, we’ll look at the general solution. Let $p$ denote the probability the drunkard takes a step towards the cliff and $(1-p)$ the probability the drunkard takes a step away from the cliff. Replacing $1/3$ with $p$ and $2/3$ with $(1-p)$ in (1) gives the quadratic equation:
$$p_{1} = p + (1-p) p^{2}_{1}.$$Finding the solutions of this equation gives:
$$p_{1} = \frac{1 \pm \sqrt{1 - 4(1-p)p}}{2(1-p)},$$$$\begin{equation}p_{1} =\{ 1, \frac{p}{(1-p)} \},\end{equation}$$In the case $p = 1$, equation (2) gives $p_{1} = \{1, \infty \}$. Due to the axioms of probability (see appendix), $p_{1}$ must be 1 when $p=1$. If $p = 0$, equation (2) gives $p_{1} = \{0, 1\}$. Intuitively, 0 must be the correct solution here.
In general, we know for any 2D random walk, every point is revisited infinitely many times, so $p_{1} = 1$ for $p \geq 1/2$.
Plotting the probabilities for $p_{1}$ for a range of values for $p$ gives:
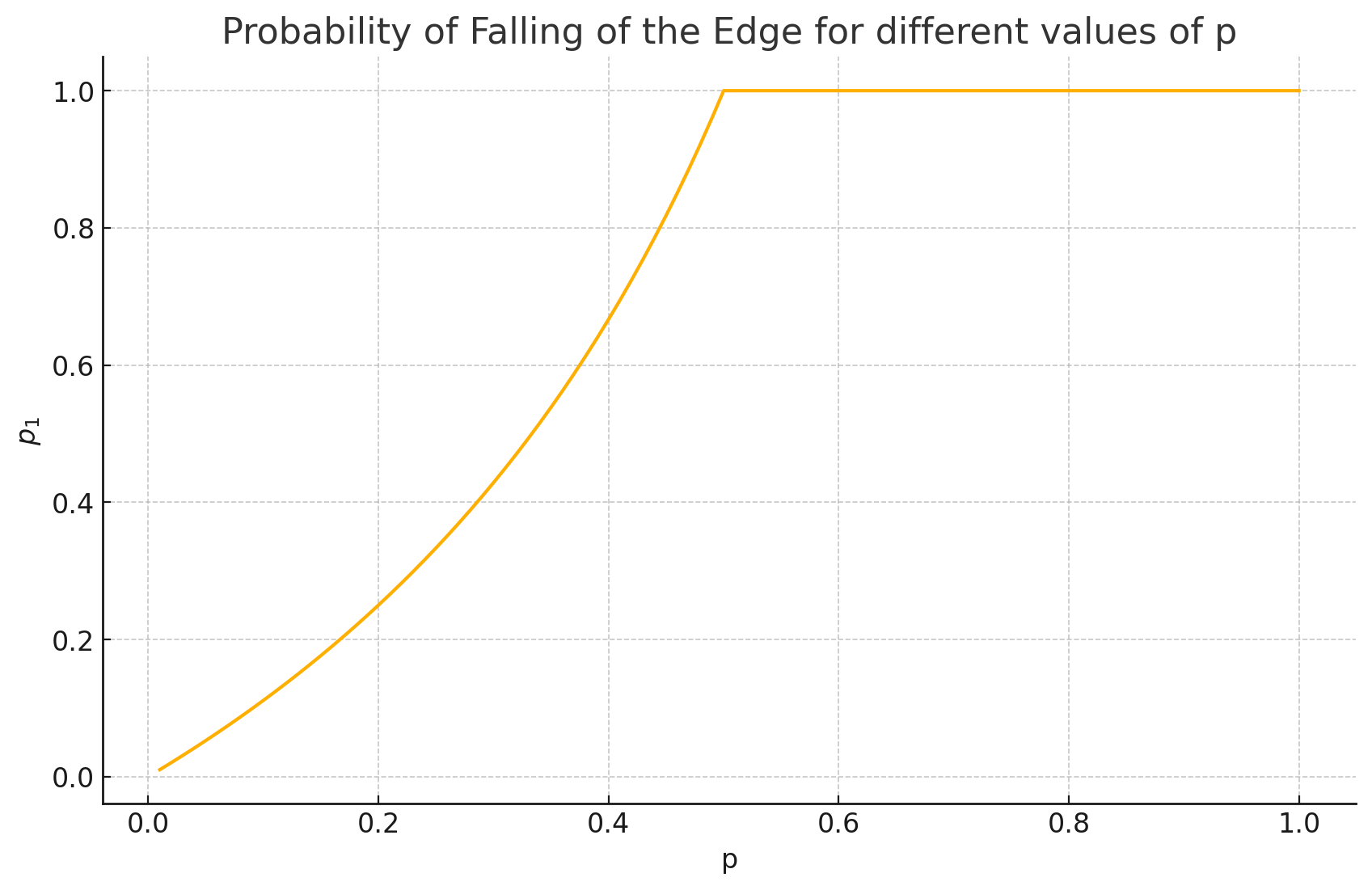
Consequently, if the drunkard had $p = 1/3$, they would have a $1/2$ chance of not falling off the edge.
N Points on a Circle
Given N points are drawn randomly on the circumference of a circle, what is the probability they are all drawn within the same semicircle.
For this question, we will create a random variable called $A_i$ which denotes the event where all the other N-1 points except point i fall in the clockwise semi circle starting at point i.
For any index i, the probability that all other points fall in this clockwise semi-circle is $\frac{1}{2^{N-1}}$.
The key observation of this problem is that the probability that event $A_i$ and $A_j$ occurs when $i \neq j$ is 0 because these events are mutually exclusive. All the points in the clockwise direction of I cannot also fall in the clockwise direction of starting from point j. Consequently, these events must be mutually exclusive.
$$\mathbb{P}[\cup_{I=1}^N A_i] = \sum_{I=1}^N \mathbb{P}[A_i] = N . 1/ 2^{N-1} = N / 2^{N-1}.$$This same argument also applies to arcs of less than 1/2 the circumference of the circle.
To prove this works, they the example we have two points. Intuitively, the probability both these points fall in the same semi-circle is 1. Applying the method discussed above will also provide an output of 1.
Cars on a Road
Suppose the probability of observing one or more cars on the road during a 20 minute interval is 609/625. What is the probability of observing 1 or more cars in a 5 minute interval.
Let $X_{0:20}$ denote the random variable for the number of cars during this 20 minute interval. Similarly, $X_{0:5}$, $X_{5:10}$, $X_{10:15}$, and $X_{15:20}$ be random variable from time 0 to 5, etc and $X_{0:20} = X_{0:5} + X_{5:10} + X_{10:15} + X_{15:20}$.
From the problem question, we know that the probability of not observing a car during the 20 minute interval is $1 - \frac{609}{625} = \frac{16}{625}$. This event only occurs when intervals $X_{0:5} =0, X_{5:10}=0, X_{10:15} = 0,$ and $X_{15:20}=0$. Using the fact that each of these intervals are i.i.d.
$$\begin{align*}\mathbb{P}[X_{0:20} = 0] &= \mathbb{P}[X_{0:5} + X_{5:10} + X_{10:15} + X_{15:20} = 0] \\ &= \mathbb{P}[X_{0:5}=0] * \mathbb{P}[X_{5:10} = 0] * \mathbb{P}[X_{10:15} = 0] * \mathbb{P}[X_{15:20} = 0] \\ &= \mathbb{P}[X_{0:5}=0]^4 = \frac{16}{625} \end{align*}$$This implies
$$\mathbb{P}[X_{0:5}=0] = \frac{2}{5}$$Consequently, the probability of observing 1 or more cars is:
$$\mathbb{P}[X_{0:5}\geq 1] = 1- \mathbb{P}[X_{0:5} = 0] = \frac{3}{5}$$