Image Image by Vivek Kumar

The Question

A couple chooses to keep having children till they have an equal number of boys and girls. How many children will they have on average? [1]

In this article we will cover 2 ways to solve this problem. First using a random walk and proof by contradiction. The second is Optiver’s solution to this problem which use Dyck’s path.

Solution 1

Let $X_t$ denote the random variable for which child has been born at time $t$.

Given the first child is already born at time 0. If the first child is a boy, then let $X_t$ take the value 1 if a boy is born at time t and let $X_t$ be -1 if a girl is born at time t. Similarly, if the first child is a girl, then $X_t$ will take the value 1 if a girl is born at time t and we will take the value -1 if a girl has been born at time t.

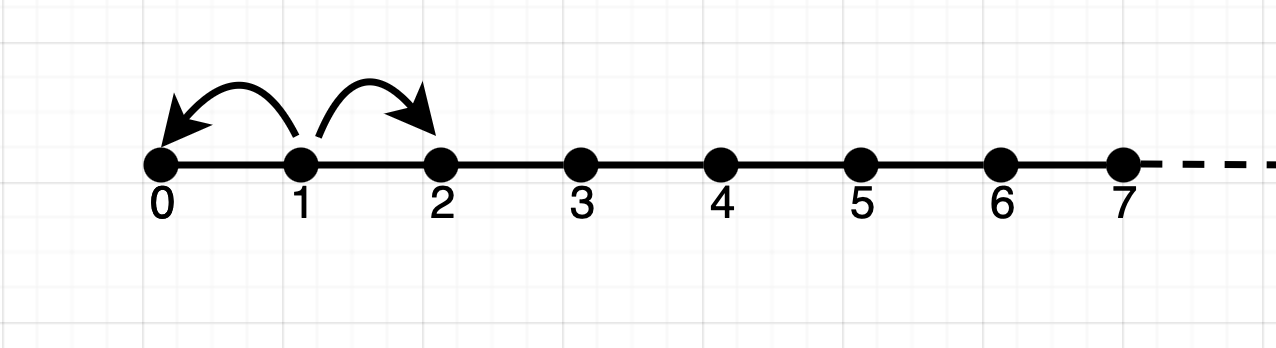
Using the random variable $X_t$, we can model this question as a 1D random walk starting at the point 1. Image

Without loss of generality, we will assume the first child to be born is a boy. If the next child born is a boy, we go up one, otherwise we go down one.

$$X_t = \begin{cases} 1 \quad &w.p. 1/2 \ \ (\text{if a boy}) \\ -1 \quad &w.p. 1/2 \ \ (\text{if a girl})\end{cases}$$

The random walk will finish once we hit 0 (i.e. when we have had equal number of boys and girls).

Now, let $W_x$ denote the number of walks starting from x to reach 0. More specifically, $W_x$ is the first time, given we have started at x, to hit 0.

$$\sum_{i=x}^{W_x} X_i = 0$$

Our goal is to determine $\mathbb{E}[W_1]$, i.e. the number of children needed to have an equal number of boys and girls, given that our first child is a boy.

Spoiler warning. The answer is infinite and to prove this we will use a proof by contradiction. Given we are at step 1, let us suppose that $\mathbb{E}[W_1]$ is finite. Following this assumption and the formula for expectation:

$$\begin{align*}\mathbb{E}[W_1] &= \mathbb{P}[X_1 = -1] \mathbb{E}[W_1 | X_1 = -1] + \mathbb{P}[X_1 = 1] \mathbb{E}[W_1 | X_1 = 1] \\ &=\frac{1}{2}(1 + \mathbb{E}[W_0]) + \frac{1}{2}(1 + \mathbb{E}[W_2]) \\ &= 1 + \frac{1}{2}\mathbb{E}[W_2]\end{align*}$$

Given you are at step 2, returning back to step 1 is equivalent to being at step 1 and returning to step 0, i.e., they are identically distributed.

$$\mathbb{E}[W_2] = \mathbb{E}[W_1] + \mathbb{E}[W_1]$$

By substitution, we get:

$$\begin{align*}\mathbb{E}[W_1] &= 1 + \frac{1}{2}(\mathbb{E}[W_1] + \mathbb{E}[W_1]) \\ &= 1 + \mathbb{E}[W_1]\end{align*}$$

This is a contradiction! As a result, the expected number of children to have before you hit 0 is infinite.

Solution 2

For this solution, we’ll start with the formula for the expectation of a discrete random variable.

$$\mathbb{E}[X] = \sum x . \mathbb{P}[X = x]$$

In our case, let $X$ be the random variable denoting the number of children needed to reach parity. We can then rewrite the formula above as:

$$\mathbb{E}[X] = \sum_{x=2}^\infty x . \mathbb{P}[X = x]$$

To solve this formula, we need to find $\mathbb{P}[X = x]$ for each value of $x$. To do this, we will model this question as a 2D random walk. Lets take $x=10$ as an example and we’ll use the grid below. 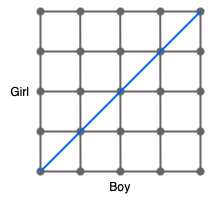Image Anytime the couple gives birth to a boy, a step to the right is taken and if a girl is birthed, a step up is taken. Equality is reached when the path hits the blue line.

Representing the question using a 2d grid now opens the possibility of using something called Dyck’s path [2]. A Dyck path is a staircase walk from (0,0) to (n,n) that lies strictly below (but may touch) the diagonal y=x. The number of Dyck’s paths of order n is given by the Catalan number:

$$C_n = \frac{1}{n+1} \binom{2n}{n}.$$

If the first child is a boy and we are looking at the paths to hit equality by child 10, then we know the final step must be a girl. 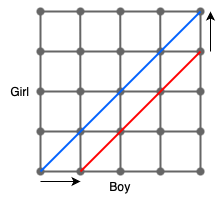Image Using this methodology, any path from the first boy to the last girl which touches but does not surpass the red line, is a valid path. This allows us to use Dyck’s path of degree 4.

$$C_4 = \frac{1}{5} \binom{8}{4} = 14$$

Consequently, the number of paths that start with a boy and achieves equality on the 10th child is 14. By symmetry, the number of paths that start with a girl and achieves equality on the 10th child is also 14.

To convert this to a probability, we will divide by the total number of possible paths by the 10th child, which is $2^{10} = 1024$. So the probability of achieving equality of the 10th child is:

$$\mathbb{P}[X=10] = \frac{14 + 14}{1024} = \frac{28}{1024}.$$

Now, lets do the rest. Let $x=2k$ where $k\in \mathbb{Z}^+$.

$$\begin{align*} \mathbb{P}[X = 2k] &= \frac{2 C_{k-1}}{2^{2k}} \\ &= \frac{2}{k}\binom{2k-2}{k-1}\frac{1}{2^{2k}} \\ &= \frac{2}{4^kk} \binom{2k-2}{k-1}\end{align*}$$

By substitution:

$$\begin{align*}\mathbb{E}[X] &= \sum_{k=1}^\infty 2k . \mathbb{P}[X = 2k] \\ &= \sum_{k=1}^{\infty} 2k \frac{2}{4^kk} \binom{2k-2}{k-1} \\ &= \sum_{k=1}^{\infty} \frac{1}{4^{k-1}} \binom{2k-2}{k-1} \end{align*}$$

Substituting $n = k-1$ gives:

$$\begin{align*}\mathbb{E}[X] &= \sum_{n=0}^{\infty} \frac{1}{4^n} \binom{2n}{n} \end{align*}$$

Using the fact that:

$$4^n = 2^{2n} = (1 + 1)^{2n} = \sum_{m=0}^{2n} \binom{2n}{m} < (2n + 1) \binom{2n}{n}$$$$\frac{1}{4^n} \binom{2n}{n} > \frac{1}{2n+1}$$$$\begin{align*}\mathbb{E}[X] &= \sum_{n=0}^{\infty}\frac{1}{4^n} \binom{2n}{n} \\ &> \sum_{n=0}^\infty\frac{1}{2n+1} \\ &> \sum_{n=0}^\infty \sum{1}{2n} \\ &= \frac{1}{2} \sum_{n=0}^\infty \frac{1}{n} \\ &\rightarrow \infty \end{align*}$$

As a result, the expectation is infinite!

References

  1. Optiver (2024). Prove it - Ep5: Perpetual Children. [online] YouTube. Available at: https://www.youtube.com/watch?v=YllN9Pz15cU [Accessed 22 Dec. 2024].
  2. Weisstein, Eric W. “Dyck Path.” Mathworld.wolfram.com, 18 Dec. 2024, mathworld.wolfram.com/DyckPath.html.